About Me
As a native of St. Louis, MO, I love all things St. Louis,
especially the beer, the Imo's Pizza, and the sports teams.
The St. Louis Blues hold a special place in my heart, and I
eagerly await their first Stanley Cup. Being a Notre Dame
football fan has made me almost too good at waiting for a
championship, but there’s always next year, right? While not
working on my simulations, you can find me either watching
sports or playing foosball.
Education:
I graduated from the University of Notre Dame in 2014 with a
Bachelor of Science with a major in Physics and concentrations
in Astrophysics and Advanced Physics. I earned my Master's in Science from UW in 2016
and became a PhD Candidate in the Fall of 2018. I expect to graduate
with my PhD in Astronomy in the summer of 2020.
Research
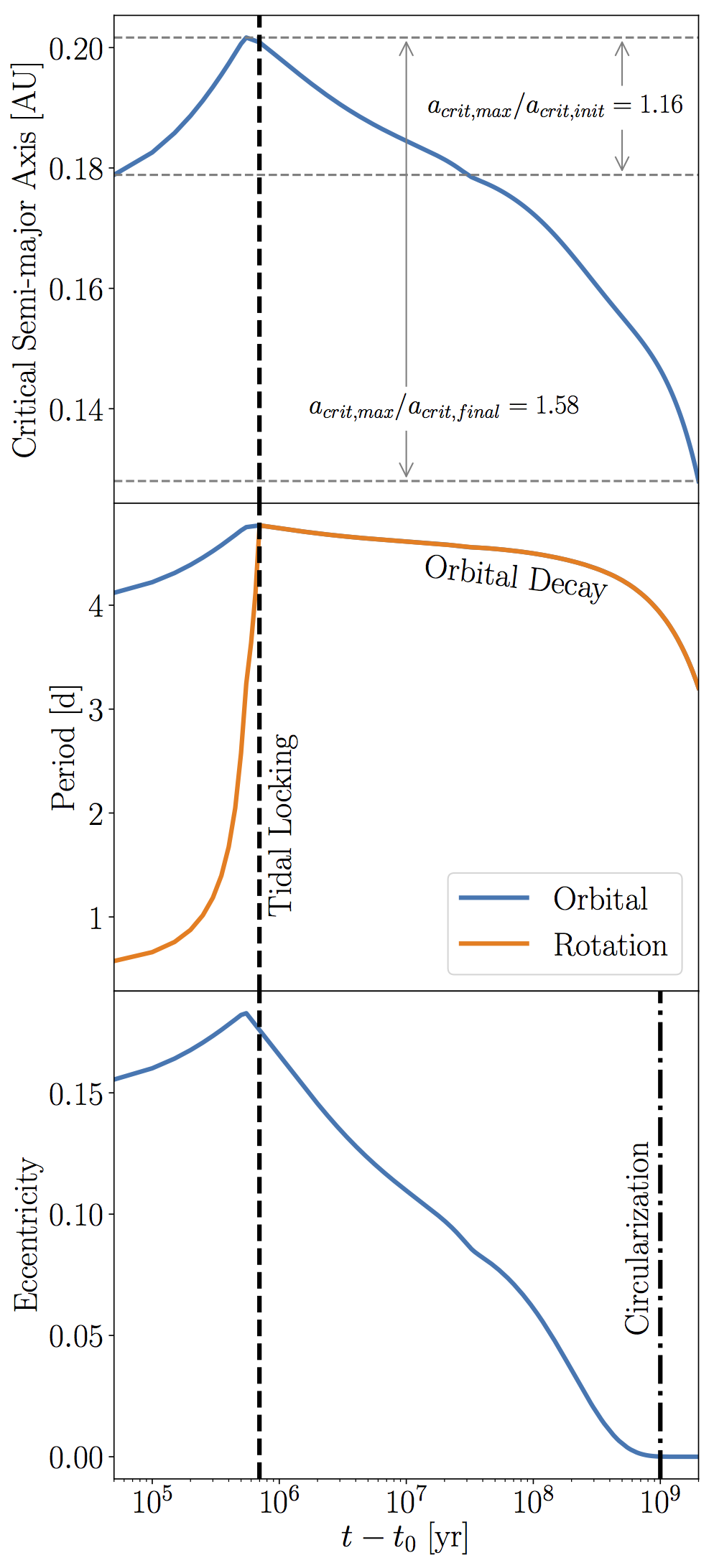
On the Lack of Circumbinary Planets Orbiting Isolated Binary Stars
In this paper, we outlined a mechanism that explains the observed lack of circumbinary
planets (CBPs) via coupled stellar-tidal evolution of isolated
binary stars. Tidal forces between low-mass, short-period binary
stars on the pre-main sequence slow the stellar rotations
transferring rotational angular momentum to the orbit as the stars
approach the tidally locked state. This transfer increases the binary
orbital period, expanding the region of dynamical instability
around the binary, and destabilizing CBPs that tend to preferentially
orbit just beyond the initial dynamical stability limit. After
the stars tidally lock, we find that angular momentum loss due to
magnetic braking can significantly shrink the binary orbit, and
hence the region of dynamical stability, over time, impacting
where surviving CBPs are observed relative to the boundary. We
perform simulations over a wide range of parameter space and find
that the expansion of the instability region occurs for most
plausible initial conditions and that, in some cases, the stability
semimajor axis doubles from its initial value. We examine the
dynamical and observable consequences of a CBP falling within the
dynamical instability limit by running N-body simulations of
circumbinary planetary systems and find that, typically, at least
one planet is ejected from the system. We apply our theory to
the shortest-period Kepler binary that possesses a CBP, Kepler-47,
and find that its existence is consistent with our model. Under
conservative assumptions, we find that coupled stellar-tidal
evolution of pre-main sequence binary stars removes at least one
close-in CBP in 87% of multi-planet circumbinary systems.
Check out the ApJ paper, Fleming et al. (2018), here!
Coevolution of Binaries and Gaseous Discs
The recent discoveries of circumbinary planets by Kepler raise
questions for contemporary planet formation models. Understanding
how these planets form requires characterizing their formation
environment, the circumbinary protoplanetary disc, and how the
disc and binary interact and change as a result. The central
binary excites resonances in the surrounding protoplanetary disc
that drive evolution in both the binary orbital elements and in
the disc. To probe how these interactions impact binary eccentricity
and disc structure evolution, N-body smooth particle hydrodynamics
(SPH) simulations of gaseous protoplanetary discs surrounding binaries
based on Kepler 38 were run for 104 binary periods for several
initial binary eccentricities. We find that nearly circular binaries
weakly couple to the disc via a parametric instability and excite
disc eccentricity growth. Eccentric binaries strongly couple to
the disc causing eccentricity growth for both the disc and binary.
Discs around sufficiently eccentric binaries that strongly couple
to the disc develop an m=1 spiral wave launched from the 1:3 eccentric
outer Lindblad resonance (EOLR) that corresponds to an alignment
of gas particle longitude of periastrons. All systems display
binary semimajor axis decay due to dissipation from the viscous disc.
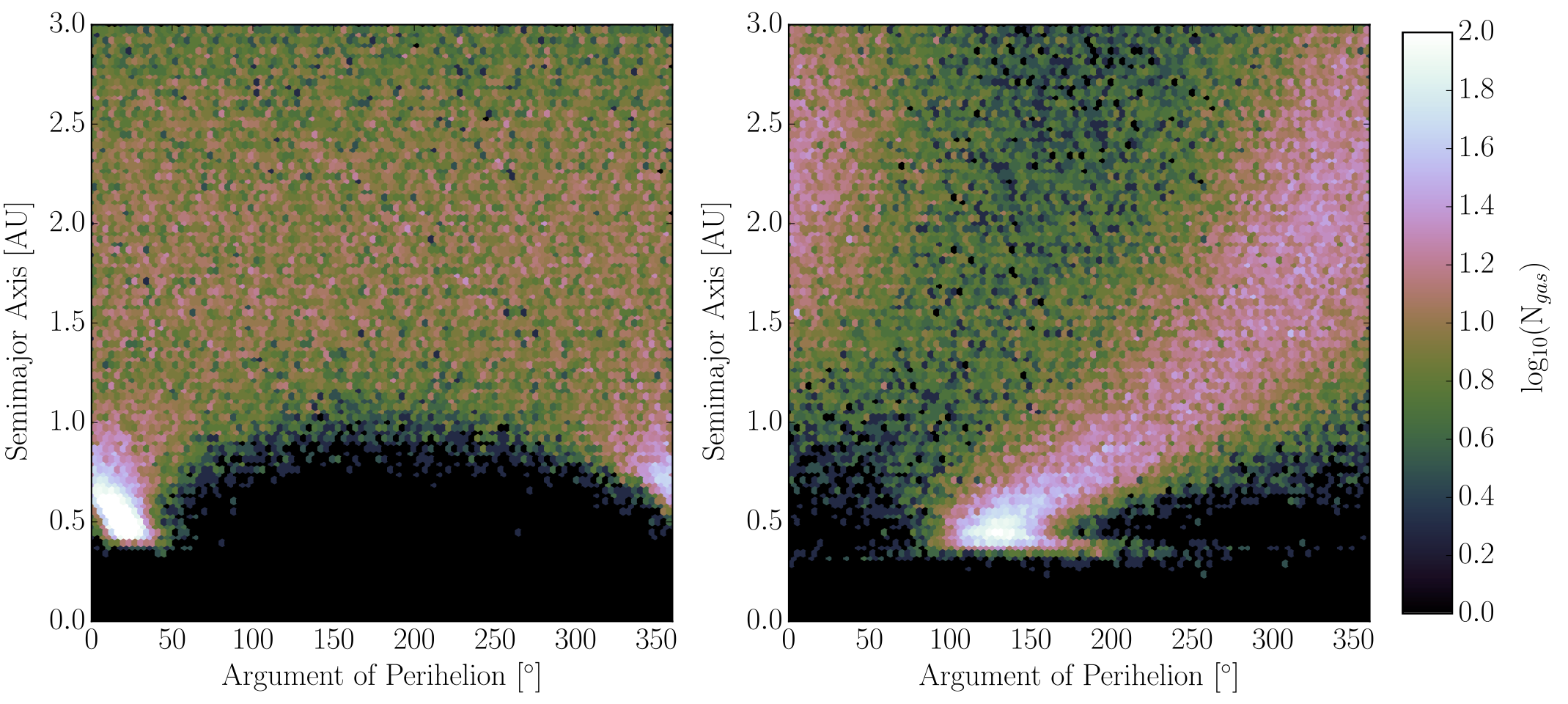
Check out the MNRAS paper, Fleming & Quinn (2017), here!
approxposterior: machine learning stellar and exoplanet dynamics
The code is open-source and publicly available on GitHub!
A common task in science or data analysis is to perform Bayesian
inference to derive a posterior probability distribution for
model parameters conditioned on some observed data with uncertainties.
In astronomy, for example, it is common to fit for the stellar
and planetary radii from observations of stellar fluxes as a
function of time using the Mandel & Agol (2002) transit model.
Typically, one can derive posterior distributions for model
parameters using Markov Chain Monte Carlo (MCMC) techniques
where each MCMC iteration, one computes the likelihood of the
data given the model parameters. One must run the forward model
to make predictions to be compared against the observations
and their uncertainties to compute the likelihood. MCMC chains
can require anywhere from 10,000 to over 1,000,000 likelihood
evaluations, depending on the complexity of the model and the
dimensionality of the problem. When one uses a slow forward model,
one that takes minutes to run, running an MCMC analysis quickly
becomes very computationally expensive. In this case,
approximate techniques are requires to compute Bayesian posterior
distributions in a reasonable amount of time by minimizing
the number of forward model evaluations.
I am the lead developer of approxposterior, a Python
implementation of Bayesian Active Learning for Posterior
Estimation by Kandasamy et al. (2015) and Adaptive Gaussian
process approximation for Bayesian inference with expensive
likelihood functions by Wang & Li (2017). These algorithms
allows the user to compute approximate posterior probability
distributions using computationally expensive forward models
by training a Gaussian Process (GP) surrogate for the likelihood
evaluation. The algorithms leverage the inherent uncertainty
in the GP's predictions to identify high-likelihood regions
in parameter space where the GP is uncertain. The algorithms
then run the forward model at these points to compute their
likelihood and re-trains the GP to maximize the GP's predictive
ability while minimizing the number of forward model evaluations.
Check out Bayesian Active Learning for Posterior Estimation by
Kandasamy et al. (2015) and Adaptive Gaussian process
approximation for Bayesian inference with expensive likelihood
functions by Wang & Li (2017) for in-depth descriptions of the respective algorithms.
Publications: Click here for all of David's publications on ADS
Contact
Email: dflemin3 (at) uw (dot) edu
Publications: Click here for all of David's publications on ADS
Elements
Text
This is bold and this is strong. This is italic and this is emphasized.
This is superscript text and this is subscript text.
This is underlined and this is code: for (;;) { ... }. Finally, this is a link.
Heading Level 2
Heading Level 3
Heading Level 4
Heading Level 5
Heading Level 6
Blockquote
Fringilla nisl. Donec accumsan interdum nisi, quis tincidunt felis sagittis eget tempus euismod. Vestibulum ante ipsum primis in faucibus vestibulum. Blandit adipiscing eu felis iaculis volutpat ac adipiscing accumsan faucibus. Vestibulum ante ipsum primis in faucibus lorem ipsum dolor sit amet nullam adipiscing eu felis.
Preformatted
i = 0;
while (!deck.isInOrder()) {
print 'Iteration ' + i;
deck.shuffle();
i++;
}
print 'It took ' + i + ' iterations to sort the deck.';
Lists
Unordered
- Dolor pulvinar etiam.
- Sagittis adipiscing.
- Felis enim feugiat.
Alternate
- Dolor pulvinar etiam.
- Sagittis adipiscing.
- Felis enim feugiat.
Ordered
- Dolor pulvinar etiam.
- Etiam vel felis viverra.
- Felis enim feugiat.
- Dolor pulvinar etiam.
- Etiam vel felis lorem.
- Felis enim et feugiat.
Icons
Actions
Table
Default
| Name |
Description |
Price |
| Item One |
Ante turpis integer aliquet porttitor. |
29.99 |
| Item Two |
Vis ac commodo adipiscing arcu aliquet. |
19.99 |
| Item Three |
Morbi faucibus arcu accumsan lorem. |
29.99 |
| Item Four |
Vitae integer tempus condimentum. |
19.99 |
| Item Five |
Ante turpis integer aliquet porttitor. |
29.99 |
|
100.00 |
Alternate
| Name |
Description |
Price |
| Item One |
Ante turpis integer aliquet porttitor. |
29.99 |
| Item Two |
Vis ac commodo adipiscing arcu aliquet. |
19.99 |
| Item Three |
Morbi faucibus arcu accumsan lorem. |
29.99 |
| Item Four |
Vitae integer tempus condimentum. |
19.99 |
| Item Five |
Ante turpis integer aliquet porttitor. |
29.99 |
|
100.00 |


